EL TEOREMA DE NORTON dice que cualquier parte de un circuito formada por fuentes y resistencias puede ser reemplazado por una única fuente de corriente y una resistencia en paralelo. De este teorema podemos deducir que cualquier circuito equivalente de Thévenin también puede ser reemplazado por un equivalente de Norton. El Teorema de Norton consiste en la misma idea del teorema de Thévenin, pero el objetivo de este es reducir el circuito a una sola resistencia en paralelo con una fuente de corriente constante.
El Teorema de Norton afirma que:“Cualquier circuito lineal que contenga varias fuentes de energía y resistencias puede ser reemplazado por una única fuente de corriente constante en paralelo con una resistencia. Un circuito que tenga dos terminales, se comporta respecto de una resistencia de carga colocada entre ellos como un simple generador de intensidad IN en paralelo con una resistencia RN“.
Teniendo como componentes principales del circuito equivalente:
RL: Se refiere a la resistencia de carga que se conecta al circuito simplificado.
RN: Es la resistencia equivalente que se ha calculado a partir de un circuito más complejo.
IN: Es la corriente equivalente del circuito inicial.
La resistencia de Norton tiene el mismo valor que la resistencia de Thévenin. La corriente de Norton se calcula como la corriente que circula por el equivalente de Thévenin poniendo en cortocircuito a los terminales A y B, es decir VTH/RTH.
El teorema de Norton es aplicado en el cálculo y diseño de circuitos eléctricos, en 1926 fue publicado por vez primera por un ingeniero de los Laboratorios Bell llamado Edward Lawry Norton. Al ser sustituida una fuente de corriente por una de tensión el terminal positivo de la fuente de corriente tiene que coincidir con el terminal positivo de la fuente de tensión en el momento de aplicar el teorema de Norton. En esencia el teorema de Norton permitirá simplificar un circuito comprendido entre dos terminales.
Enunciado del Teorema
Circuito Equivalente de NortonEs el recíproco del Teorema de Thevenin y dice:"Todo circuito compuesto de generadores y resistencias se puede reemplazar por un generador de corriente IN en paralelo con una resistencia RN ".Dónde IN es igual a la corriente que circula por los terminales de salida cuando estas se ponen en cortocircuito. RN es la misma que la de Thevenin.
Procedimiento para aplicar el Teorema de Norton
El procedimiento básico para resolver un circuito usando el Teorema de Norton es el siguiente:
El procedimiento básico para resolver un circuito usando el Teorema de Norton es el siguiente:
1-. Retirar la resistencia de carga RL o la red del circuito correspondiente.
2-. Encontrar RN cortocircuitando todas las fuentes de voltaje o abriendo el circuito de todas las fuentes de corriente.
3-. Encontrar IN por los métodos habituales de análisis de circuitos mediante la colocación de un corto circuito en las terminales A y B.
4-. Encontrar la corriente que fluye a través de la resistencia de carga RL.
Vemos que tras cortocircuitar los terminales A y B, las dos resistencias se encuentran conectadas en paralelo a través de sus dos fuentes de tensión. En base a ello, calculamos la corriente que fluye por cada resistencia, así como la corriente total de cortocircuito (IN):
Conociendo la corriente de cortocircuito IN y la resistencia equivalente RN, podemos montar el circuito equivalente de Norton:
El siguiente paso será resolver el problema con la resistencia de carga original de 40 Ω y así poder ver la caída de tensión A-B y la corriente que circula por RL.
Calcular la resistencia total (RT) calculando el paralelo de las dos resistencias:
Hallar la caída de tensión entre A y B (VAB), es decir, la caída de voltaje en RL:
Finalmente calcular la corriente que circula por RL:
Por tanto, en Thévenin tendríamos una fuente de voltaje de 13.33 V conectada en serie a una resistencia de 6.67 Ω, tal y como hemos visto en el otro teorema explicado.
El Teorema de Norton es una forma de reducir una red a un circuito equivalente compuesto por una única fuente de corriente, resistencia paralela y carga paralela.
Características del Teorema de Norton
1-. El nuevo y más simple circuito permite llevar a cabo cálculos rápidos de voltaje, corriente o potencia que el circuito es capaz de entregar a la carga RL.
2-. Este teorema se puede aplicar a cualquier elemento del circuito.
3-. El teorema de Norton, hace más fácil cualquier tipo de circuito, su finalidad es esa, facilitar.
3-. El teorema de Norton, hace más fácil cualquier tipo de circuito, su finalidad es esa, facilitar.
Convertir de Norton a Thévenin
Los equivalentes de Thévenin y Norton son independientes de la red del circuito restante que representa una carga. Esto permite hacer cambios en la carga sin volver a analizar los equivalentes de Thévenin o Norton.
Los equivalentes de Thévenin y Norton son independientes de la red del circuito restante que representa una carga. Esto permite hacer cambios en la carga sin volver a analizar los equivalentes de Thévenin o Norton.
Thévenin a Norton
Para poder convertir de Thévenin a Norton únicamente debemos aplicar la ley de ohm para encontrar la corriente y la fuente resultante (Fuente de corriente) se deberá poner en paralelo a la resistencia equivalente RTH
Norton a Thévenin
Para poder convertir de Norton a Thévenin únicamente debemos aplicar la ley de ohm para encontrar el voltaje y la fuente resultante (Fuente de Voltaje) se deberá poner en serie a la resistencia equivalente RTH
NOTA: Es importante considerar que la resistencia de Thévenin y la resistencia de Norton es la misma.
Ejercicio #1: Al momento de resolver circuitos eléctricos mediante el Teorema de Norton, hay 2 métodos para realizarlos. El primero consiste en considerar los valores calculados con el Teorema de Thévenin, puesto que el de Norton es el Dual, por lo que hay mucha relación; éste método suele ser más rápido, cómodo y corto, siempre y cuando se domine el teorema de Thévenin. Por otra parte, el segundo método consiste en realizar todo el procedimiento desde el principio, sin guiarnos con los cálculos de Thévenin.
En este ejercicio consideraremos el mismo circuito realizado en el Teorema de Thévenin, guiándonos por el primer método:
Queremos encontrar el circuito equivalente de Norton entre los terminales A y B, así que para ello primero tenemos que “quitar” la resistencia central de 40 Ω y aplicar los siguientes pasos:
Cortocircuitar los terminales A y B y hallar la corriente de cortocircuito (IN)
Vemos que tras cortocircuitar los terminales A y B, las dos resistencias se encuentran conectadas en paralelo a través de sus dos fuentes de tensión. En base a ello, calculamos la corriente que fluye por cada resistencia, así como la corriente total de cortocircuito (IN): 
Cortocircuitar las fuentes y eliminar la resistencia que hay entre los terminales para hallar RN
Si ponemos a 0 V (en corto) las dos fuentes de tensión y los terminales A y B los ponemos en circuito abierto, vemos que las dos resistencias se conectan en paralelo.
El valor de la resistencia interna RN se obtiene calculando la resistencia total en los terminales A y B dándonos el siguiente circuito:
El siguiente paso será resolver el problema con la resistencia de carga original de 40 Ω y así poder ver la caída de tensión A-B y la corriente que circula por RL.
Calcular la resistencia total (RT) calculando el paralelo de las dos resistencias:
La corriente de carga y la caída de voltaje entre A y B es la misma que dio en el ejercicio realizado mediante el Teorema de Thevenin.
Por otro lado, si desea pasar de un circuito de Thevenin a uno Norton o viceversa, únicamente deberá de aplicar la Ley de Ohm:
Por tanto, en Thévenin tendríamos una fuente de voltaje de 13.33 V conectada en serie a una resistencia de 6.67 Ω, tal y como hemos visto en el otro teorema explicado.
El Teorema de Norton es una forma de reducir una red a un circuito equivalente compuesto por una única fuente de corriente, resistencia paralela y carga paralela.
Ejercicio #2:
En este caso emplearemos el método #2, el cuál es realizar los cálculos partiendo desde el principio, y no basándonos en lo calculado con Thévenin. Este procedimiento es más largo, engorroso y confuso, sin embargo es igual de preciso.
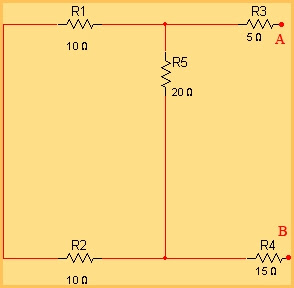
Obtener el equivalente Norton, entre los terminales A y B, del circuito de la figura y la intensidad que circula por la resistencia de carga RL=10Ω.
Lo primero que haremos será cortocircuitar la resistencia de carga, quedando un circuito como el siguiente:
Este circuito lo podemos resolver por cualquiera de los métodos de resolución conocido. Sin embargo, en este caso hemos optado por resolverlo mediante mallas.
Fijamos las intensidades de malla y planteamos las ecuaciones correspondientes.
Despejando IB de la primera ecuación y sustituyendo en la segunda.
Obtenemos el siguiente resultado:
El valor de la resistencia equivalente entre los terminales A y B se obtendrá cortocircuitando los generadores existentes. El circuito sería el siguiente:
Tenemos que R1 y R2 están en serie, por tanto:
Esta resistencia resultante se encuentra en paralelo con R5, por lo tanto:
Por otra parte R3 y R4 también están en serie:
Una vez calculado, nos queda que R125 y R34 están en serie, por lo que:
Por tanto el equivalente de Norton nos queda como:
Si entre los terminales A y B colocamos una resistencia de carga de RL=10Ω, la intensidad que circule por esta resistencia será:
Aplicaciones del Teorema de Norton
El Teorema de Norton es útil en el análisis del circuito de sistemas de intensidades de corrientes múltiples.
Al igual que el teorema de Thévenin, en los sistemas eléctricos grandes, por ejemplo, se utiliza la reducción mediante el Teorema de Norton para el cálculo de corrientes máximas en condiciones de falla (cortocircuitos) en las redes (y así calcular y coordinar sus protecciones), ya que se puede representar a todo el sistema de un país con una simple fuente de voltaje con una impedancia en serie.
La aplicación de este teorema es muy importante y común, ya que con ayuda del teorema de Thévenin es más fácil predecir el comportamiento de un sistema en condiciones de falla y existe la coordinación (por ejemplo, si en una casa hubiera un cortocircuito se tendría que dejar fuera todo el sistema).
Lo principal es su propio enunciado, la reducción de circuitos y redes complejas a una forma simple que permite un análisis de mayor comodidad y rapidez. Es utilizado en redes eléctricas de Potencia, para análisis de estabilidad de la red y localización de fallas. Se utiliza en la caracterización (o sea, determinación de parámetros) de semiconductores, dispositivos piezoeléctricos, entre otros.